
Refining the algorithms used to train computers makes Machine Learning more accurate.
Behind facial recognition, driverless cars, and virtual assistants is Deep Learning—a Machine Learning technology that imitates how the human brain learns using multiple layers of networks. These networks are collections of interconnected nodes that mimic biological neurons. The driving force behind these networks are mathematical algorithms, which draw on data to train computers and create predictive models. Training machines is an iterative process—with each iteration, the model grows more complex and more accurate—and that accuracy is driven by underlying mathematical algorithms.
Theory Behind the Tech
To make strides towards achieving the breakthroughs Deep Learning is capable of, University of Guelph Mathematics professor, Dr. Mihai Nica [1] and colleagues have presented cutting-edge research on a type of neural network called Residual Neural Networks—ResNets—at the 35th Conference on Neural Information Processing Systems. ResNets are models that add extra connections between layers in Deep Neural Networks, improving accuracy and performance.
This study builds on a breakthrough in the field of Deep Learning: algorithms that allowed the width of the neural network—the number of nodes within a layer—to grow infinitely. Nica and his colleagues noticed that, while applying infinite limits to width helped improve accuracy, the depth of the network (the number of layers) was still treated as a static value. The team set out to explore what happens when both depth and width of the network are treated with infinite limits.
A Simple Adjustment with Big Impacts
The team applied mathematical techniques to adjust the algorithms and found that their theory provided more accurate predictions of the network properties than the previous model that only accounted for infinite width.
In the process, their analysis also revealed that ResNets demonstrated “hypoactivation,” where less than half of the artificial neurons were activated when the algorithms are initialized. To deal with this roadblock, the team developed a technique that corrects the hypoactivation.
“Our work shows that as depth increases, neural networks behave differently than the predictions of the older theory that assumes the depth is small compared to the network width” says Nica. “Despite how popular neural nets are, understanding why neural networks perform the way they do is still a huge mystery. Theoretical work like this puts us closer to understanding what is going on and hopefully unlocking even more powerful neural networks in the future.”
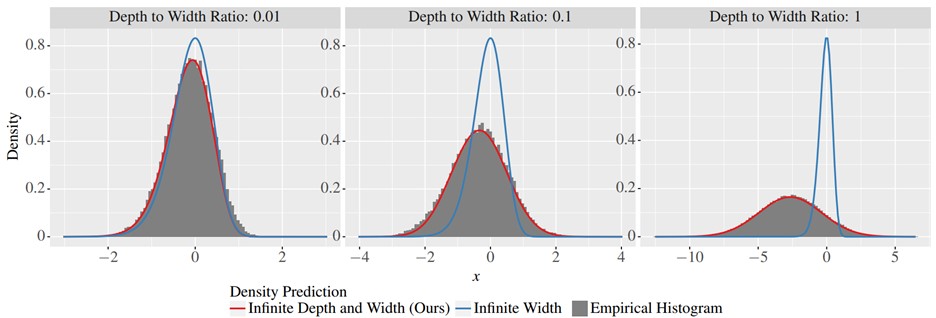
The result of computer simulations shown as a grey histogram. The new theory predicts the red curve, which accounts for the depth and width ratio. This matches the experiments more closely for deeper networks than the older infinite-width theory shown in the blue curve.
A video introduction to this new type of infinite depth limit is available:

Mihai Nica is an assistant professor in the Mathematics and Statistics Department.
This work was supported by a Natural Sciences and Engineering Research Council (NSERC) Discovery Grant.
Li MB, Nica M, Roy DM. The Future is Log-Gaussian: ResNets and Their Infinite-Depth-and-Width Limit at Initialization [2]. NeurIPS Conference on Neural Information Processing Systems. 6 Dec 2021.